

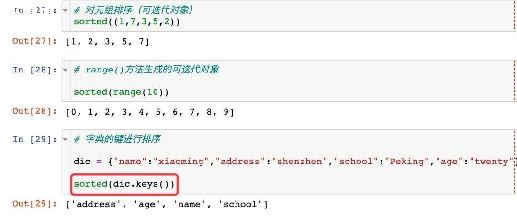
#递归
def?power(n,?x):
return?0#回归条件
else:
m?=?n?+?1#递归因子

return?1/pow(n,?x)+power(m,?x)#求和奇正
return?-1/pow(n,?x)+power(m,?x)#求和偶负
sum?=?0
sum+=?1?/?pow(n,?x)
sum+=-1?/?pow(n,?x)
n?+=?1?#?递增
return?sum
if?__name__?==?"__main__":
x?=?input("请输入幂数")
x?=?int(x)
n?=?1
sum?=?power(n,?x)
print(sum)
n=1
递归的思想主要是能够重复某些动作,比如简单的阶乘,次方,回溯中的八皇后,数独,还有汉诺塔,分形.
由于堆栈的机制,一般的递归可以保留某些变量在历史状态中,比如你提到的return x * power..., 但是某些或许庞大的问题或者是深度过大的问题就需要尽量避免递归,因为可能会栈溢出.还有一个问题是~python不支持尾递归优化!!!!所以~还是尽量避免递归的出现.
def power(x, n)
if n 0:
return 1
return x * power(x, n - 1)
当函数形参n=0的时候,开始回退~直到第一次调用power结束.
①.、写出临界条件
代码实现如下:
第一种:用sum函数.
sum(lst)
第二种:循环方式.
def customer_sum(lst):
result = 0
for x in lst:
result+=x
return result
while lst:
temp = lst.pop(0)
result+=temp
if name ==" main ":
print customer_sum(lst)
第三种:递推求和
def add(lst,result):
if lst:
temp+=result
return add(lst,temp)
print add(lst,0)
第四种:reduce方式
print reduce(lambda x,y:x+y,lst)
print reduce(lambda x,y:x+y,lst,0)
def add(x,y):
return x+y
print reduce(add, lst)
print reduce(add, lst,0)
第一种:for循环判断
def statistics(lst):
dic = {}
for k in lst:
if not k in dic:
dic[k] = 1
dic[k] +=1
return dic
print(statistics(lst))
第二种:比较取巧的,先把列表用set方式去重,然后用列表的count方法
m = set(lst)
for x in m:
dic[x] = lst.count(x)
第三种:用reduce方式
def statistics(dic,k):
print reduce(statistics,lst,{})
或者
d = {}
d.extend(lst)
print reduce(statistics,d)
通过上面的例子发现,凡是要对一个集合进行操作的,并且要有一个统计结果的,能够用循环或者递归方式解决的问题,一般情况下都可以用reduce方式实现.
首先我们要了解一下什么是递归.
递归法,递归法就是利用上一个或者上几个状态来求取当前状态的值(个人看法).也可以说成函数自己调用自己的一种解决问题的策略.所以呢递归法通常是依托函数来实现的,递归函数总是会有一个出口,我们在解决递归问题时,只需要找出递归的关系式以及递归函数的出口(这两个可以说是递归函数的核心了).下面我将今天这一节举求斐波那契值的例子带领着大家具体的实践一下递归法.
递归函数的出口是当n为1时返回1,当n为0时返回0.
最后递归函数的核心代码就可以写出了:
然后总的代码就是:
具体思路如下:
因为只有第1个和第0个斐波那契值是确定的
例:
会执行第二条语句返回1值.
以上就是土嘎嘎小编为大家整理的Python函数递推罚相关主题介绍,如果您觉得小编更新的文章只要能对粉丝们有用,就是我们最大的鼓励和动力,不要忘记讲本站分享给您身边的朋友哦!!