

#二叉树的非递归遍历
①.0 function preorder($root) {
①.1 $stack = array();
①构造二叉树给定一棵二叉树,要对它进行操作必须先把它存储到计算机中,二叉树的存储可以采用顺序存储结构,也可以采用链式存储结构,链式存储结构有二叉链表和三叉链表等.今天这一节主要讨论二叉链表存储结构.
(1)以先序递归遍历思想建立二叉树.
①建立二叉树的根结点;②先序建立二叉树的左子树;③先序建立二叉树的右子树.
输入一个二叉树的先序序列,构造这棵二叉树.为了保证唯一地构造出所希望的二叉树,在键入这棵树的先序序列时,需要在所有空二叉树的位置上填补一个特殊的字符,比如#.在算法中,需要对每个输入的字符进行判断,如果对应的字符是#,则在相应的位置上构造一棵空二叉树;否则,创建一个新结点.整个算法结构以先序遍历递归算法为基础,二叉树中结点之间的指针连接是通过指针参数在递归调用返回时完成的.
//
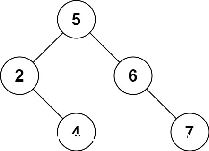
//?对应的二叉树:
//?/?\
//?/?\??/?\
#include?"stdio.h"
#include?"stdlib.h"
struct?Tree
{
int?data;
struct?Tree?*left;
struct?Tree?*right;
};
typedef?struct?Tree?TreeNode;
typedef?TreeNode?*Bitree;
typedef?struct?stack_node?//栈的结构体
Bitree?bt;
struct?stack_node?*next;
}?stack_list,?*stack_link;
Bitree?insertNode(Bitree?root,int?data)?//插入结点
Bitree?newnode;
Bitree?current;
Bitree?back;
newnode=(Bitree)malloc(sizeof(TreeNode));
if(newnode==NULL)
printf("\n动态分配内存出错.\n");
exit(1);
}
newnode-data=data;
newnode-left=NULL;
newnode-right=NULL;
if(root==NULL)
return?newnode;
else
current=root;
while(current!=NULL)
back=current;
if(current-data?data)
current=current-left;
current=current-right;
if(back-data?data)
back-left=newnode;
back-right=newnode;
return?root;
Bitree?createTree()?//创建二叉树(非递归)
Bitree?root=NULL;
int?len;
int?i;
printf("创建二叉树,请输入节点的总数量:?");
scanf("%d",len);
printf("请连续输入%d个节点的数据:?",len);
for(i=0;ilen;i++)
scanf("%d",data);
root=insertNode(root,data);
void?preOrder(Bitree?ptr)?//先序遍历(递归法)
if(ptr!=NULL)
printf("%d?",ptr-data);
preOrder(ptr-left);
preOrder(ptr-right);
void?inOrder(Bitree?ptr)?//中序遍历(递归法)
inOrder(ptr-left);
inOrder(ptr-right);
void?postOrder(Bitree?ptr)?//后序遍历(递归法)
postOrder(ptr-left);
postOrder(ptr-right);
//检查[栈]是否是空
int?isEmpty(stack_link?stack)
if(stack?==?NULL)
return?1;
return?0;
//入栈
stack_link?push(stack_link?stack,Bitree?bt)
stack_link?new_node;
new_node=(stack_link)malloc(sizeof(stack_list));
if(!new_node)
return?NULL;
new_node-bt=bt;
new_node-next=stack;
stack=new_node;
return?stack;
//出栈
stack_link?pop(stack_link?stack,Bitree?*bt)
stack_link?top;
if(isEmpty(stack))
*bt?=?NULL;
top=stack;
*bt=top-bt;
stack=top-next;
free(top);
//统计节点(非递归)
void?reportByStack(Bitree?bt,int?*pTotal,int?*pCount0,int?*pCount1,
Bitree?p=NULL;
stack_link?oneStack=NULL;
int?total=0;
int?maxValue=0,minValue=0;
if(bt?==?NULL)
return;
p=bt;??//当前二叉树的节点
minValue=p-data;
maxValue=minValue;
while(p?!=?NULL)
if(minValue?p-data)
minValue?=?p-data;
if(maxValue?p-data)
maxValue?=?p-data;
if(p-right?==?NULL?p-left?==?NULL)?//叶子
count0++;
else?//度1
count1++;
if(p-right?!=?NULL)?//如果有右子树,马上入栈
oneStack=push(oneStack,p-right);
if(p-left?!=?NULL)?//如果有左子树,设为当前节点
p=p-left;
oneStack=pop(oneStack,p);
if(p?==?NULL)
break;
*pTotal=total;
*pCount0=count0;
*pCount1=count1;
*pMaxValue=maxValue;
*pMinValue=minValue;
int?main()
root=createTree();?//创建二叉树
printf("\n前序遍历序列:?");
preOrder(root);
printf("\n中序遍历序列:?");
inOrder(root);
printf("\n后序遍历序列:?");
postOrder(root);
printf("叶子节点有%d个,数据值的最大值是%d,最小值是%d",
count0,maxValue,minValue);
printf("\n");
假如你所说的二叉树是指这种的话
那么你的数据结构一定要满足一个条件,则每一条数据必须记录好父级的标识
php
$data?=?array(
array(
'id'?=?1,
'pid'?=?0,
'name'?=?""新建脑图,
),
'pid'?=?1,
'name'?=?"分支主题",
);
foreach($data?as?$key=$value){
if(?$value['pid']?==?'0'){
$parent[]?=?$value;
unset($data[$key]);
}?
foreach($parent?as?$key=$value){
foreach($data?as?$k=$v){
if(?$v['pid']?==?$value['id']?){
$parent[$key]['_child'][]?=?$v;
unset($data[$k]);
通过以上循环过后,对应二叉树关系的数组就可以做出来了
当然上述代码只能进行到二级二叉树,如果想做出无限级二叉树的数组,则必须使用到递归函数了
PS:上述代码是网页里手打的,没经过测试,但思路肯定是没问题的哈
/**?*?二叉树的定义?*/
class?BinaryTree?{
protected?$key?=?NULL;?//?当前节点的值
protected?$left?=?NULL;??//?左子树
protected?$right?=?NULL;?//?右子树
/**?*?以指定的值构造二叉树,并指定左右子树?*
*?@param?mixed?$key?节点的值.
*?@param?mixed?$left?左子树节点.
*?@param?mixed?$right?右子树节点.
*/
public?function?__construct(?$key?=?NULL,?$left?=?NULL,?$right?=?NULL)?{
$this-key?=?$key;
if?($key?===?NULL)?{
$this-left?=?NULL;
$this-right?=?NULL;
elseif?($left?===?NULL)?{
$this-left?=?new?BinaryTree();
$this-right?=?new?BinaryTree();
else?{
$this-left?=?$left;
$this-right?=?$right;
/**
*?析构方法.
public?function?__destruct()?{
$this-key?=?NULL;
*?清空二叉树.
**/
public?function?purge?()?{
*?测试当前节点是否是叶节点.
*
*?@return?boolean?如果节点非空并且有两个空的子树时为真,否则为假.
public?function?isLeaf()?{
return?!$this-isEmpty()?
$this-left-isEmpty()?
$this-right-isEmpty();
*?测试节点是否为空
*?@return?boolean?如果节点为空返回真,否则为假.
public?function?isEmpty()?{
return?$this-key?===?NULL;
*?Key?getter.
*?@return?mixed?节点的值.
public?function?getKey()?{
if?($this-isEmpty())?{
return?false;
return?$this-key;
*?给节点指定Key值,节点必须为空
*?@param?mixed?$object?添加的Key值.
public?function?attachKey($obj)?{
if?(!$this-isEmpty())
$this-key?=?$obj;
*?删除key值,使得节点为空.
public?function?detachKey()?{
if?(!$this-isLeaf())
$result?=?$this-key;
return?$result;
*?返回左子树
*?@return?object?BinaryTree?当前节点的左子树.
public?function?getLeft()?{
if?($this-isEmpty())
return?$this-left;
*?给当前结点添加左子树
*?@param?object?BinaryTree?$t?给当前节点添加的子树.
public?function?attachLeft(BinaryTree?$t)?{
if?($this-isEmpty()?||?!$this-left-isEmpty())
$this-left?=?$t;
*?删除左子树
*?@return?object?BinaryTree?返回删除的左子树.
public?function?detachLeft()?{
$result?=?$this-left;
*?返回当前节点的右子树
*?@return?object?BinaryTree?当前节点的右子树.
public?function?getRight()?{
return?$this-right;
*?给当前节点添加右子树
*?@param?object?BinaryTree?$t?需要添加的右子树.
public?function?attachRight(BinaryTree?$t)?{
if?($this-isEmpty()?||?!$this-right-isEmpty())
$this-right?=?$t;
*?删除右子树,并返回此右子树
*?@return?object?BinaryTree?删除的右子树.
public?function?detachRight()?{
if?($this-isEmpty?())
$result?=?$this-right;
*?先序遍历
public?function?preorderTraversal()?{
return?;
echo?'?',?$this-getKey();
$this-getLeft()-preorderTraversal();
$this-getRight()-preorderTraversal();
*?中序遍历
public?function?inorderTraversal()?{
*?后序遍历
public?function?postorderTraversal()?{
*?二叉排序树的PHP实现
class?BST?extends?BinaryTree?{
*?构造空的二叉排序树
public?function?__construct()?{
parent::__construct(NULL,?NULL,?NULL);
*?析构
parent::__destruct();
*?测试二叉排序树中是否包含参数所指定的值
*?@param?mixed?$obj?查找的值.
*?@return?boolean?True?如果存在于二叉排序树中则返回真,否则为假期
public?function?contains($obj)?{
$diff?=?$this-compare($obj);
if?($diff?==?0)?{
return?true;
}elseif?($diff?0)???return?$this-getLeft()-contains($obj);
return?$this-getRight()-contains($obj);
*?查找二叉排序树中参数所指定的值的位置
*?@return?boolean?True?如果存在则返回包含此值的对象,否则为NULL
public?function?find($obj)?{
if?($diff?==?0)
return?$this-getKey();
elseif?($diff?0)???return?$this-getLeft()-find($obj);
return?$this-getRight()-find($obj);
*?返回二叉排序树中的最小值
*?@return?mixed?如果存在则返回最小值,否则返回NULL
public?function?findMin()?{
elseif?($this-getLeft()-isEmpty())
return?$this-getLeft()-findMin();
*?返回二叉排序树中的最大值
*?@return?mixed?如果存在则返回最大值,否则返回NULL
public?function?findMax()?{
elseif?($this-getRight()-isEmpty())
return?$this-getRight()-findMax();
*?给二叉排序树插入指定值
*?@param?mixed?$obj?需要插入的值.
*?如果指定的值在树中存在,则返回错误
public?function?insert($obj)?{
$this-attachKey($obj);
}?else?{
die('argu?error');
if?($diff?0)????$this-getLeft()-insert($obj);
$this-getRight()-insert($obj);
$this-balance();
*?从二叉排序树中删除指定的值
*?@param?mixed?$obj?需要删除的值.
public?function?delete($obj)?{
die();
if?(!$this-getLeft()-isEmpty())?{
$max?=?$this-getLeft()-findMax();
$this-key?=?$max;
$this-getLeft()-delete($max);
elseif?(!$this-getRight()-isEmpty())?{
$min?=?$this-getRight()-findMin();
$this-key?=?$min;
$this-getRight()-delete($min);
}?else
$this-detachKey();
}?else?if?($diff?0)????$this-getLeft()-delete($obj);
$this-getRight()-delete($obj);
public?function?compare($obj)?{
return?$obj?-?$this-getKey();
*?Attaches?the?specified?object?as?the?key?of?this?node.
*?The?node?must?be?initially?empty.
*?@param?object?IObject?$obj?The?key?to?attach.
*?@exception?IllegalOperationException?If?this?node?is?not?empty.
$this-left?=?new?BST();
$this-right?=?new?BST();
*?Balances?this?node.
*?Does?nothing?in?this?class.
protected?function?balance?()?{}
*?Main?program.
*?@param?array?$args?Command-line?arguments.
*?@return?integer?Zero?on?success;?non-zero?on?failure.
public?static?function?main($args)?{
printf("BinarySearchTree?main?program.\n");
$root?=?new?BST();
foreach?($args?as?$row)?{
$root-insert($row);
return?$root;
echo?$root-findMax();
$root-delete(100);