

将数组归一化
可以用线性归一化,就是找到最大值和最小值.
平均数是表示一组数据集中趋势的量数,是指在一组数据中所有数据之和再除以这组数据的个数.它是反映数据集中趋势的一项指标.解答平均数应用题的关键在于确定"总数量"以及和总数量对应的总份数.在统计工作中,平均数(均值)和标准差是描述数据资料集中趋势和离散程度的两个最重要的测度值.

以下为python代码,由于训练数据比较少,这边使用了批处理梯度下降法,没有使用增量梯度下降法.
##name:logReg.pyfrom numpy import *import matplotlib.pyplot as pltdef loadData(filename):
data = loadtxt(filename)
m,n = data.shape ? ?print 'the number of ?examples:',m ? ?print 'the number of features:',n-1 ? ?x = data[:,0:n-1]
y = data[:,n-1:n] ? ?return x,y#the sigmoid functiondef sigmoid(z): ? ?return 1.0 / (1 + exp(-z))#the cost functiondef costfunction(y,h):
y = array(y)
h = array(h)
J = sum(y*log(h))+sum((1-y)*log(1-h)) ? ?return J# the batch gradient descent algrithmdef gradescent(x,y):
m,n = shape(x) ? ? #m: number of training example; n: number of features ? ?x = c_[ones(m),x] ? ? #add x0 ? ?x = mat(x) ? ? ?# to matrix ? ?y = mat(y)
h = sigmoid(x*theta)
theta = theta + a * (x.T)*(y-h)
cost = costfunction(y,h)
J.append(cost)
plt.plot(J)
plt.show() ? ?return theta,cost#the stochastic gradient descent (m should be large,if you want the result is good)def stocGraddescent(x,y):
a = 0.01 ? ? ? # learning rate ? ?theta = ones((n+1,1)) ? ?#initial theta ? ?J = [] ? ?for i in range(m):
h = sigmoid(x[i]*theta)
theta = theta + a * x[i].transpose()*(y[i]-h)
plt.show() ? ?return theta,cost#plot the decision boundarydef plotbestfit(x,y,theta):
plt.xlabel('x1')
plt.show()def classifyVector(inX,theta):
m = shape(y)[0]
x = c_[ones(m),x]
y_p = classifyVector(x,theta)
accuracy = sum(y_p==y)/float(m) ? ?return accuracy
调用上面代码:
from logReg import *
x,y = loadData("horseColicTraining.txt")
theta,cost = gradescent(x,y)print 'J:',cost
ac_train = accuracy(x, y, theta)print 'accuracy of the training examples:', ac_train
x_test,y_test = loadData('horseColicTest.txt')
ac_test = accuracy(x_test, y_test, theta)print 'accuracy of the test examples:', ac_test
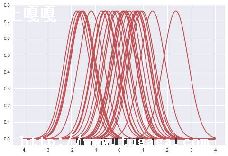
似然函数走势(J = sum(y*log(h))+sum((1-y)*log(1-h))),似然函数是求最大值,一般是要稳定了才算最好.
这个时候,我去看了一下数据集,发现没个特征的数量级不一致,于是我想到要进行归一化处理:
归一化处理句修改列loadData(filename)函数:
def loadData(filename):
max = x.max(0)
min = x.min(0)
x = (x - min)/((max-min)*1.0) ? ? #scaling ? ?y = data[:,n-1:n] ? ?return x,y
从上面这个例子,我们可以看到对特征进行归一化操作的重要性.
①.)线性归一化
这种归一化比较适用在数值比较集中的情况,缺陷就是如果max和min不稳定,很容易使得归一化结果不稳定,使得后续的效果不稳定,实际使用中可以用经验常量来代替max和min.
经过处理的数据符合标准正态分布,即均值为0,标准差为1.
经常用在数据分化较大的场景,有些数值大,有些很小.通过一些数学函数,将原始值进行映射.该方法包括log、指数、反正切等.需要根据数据分布的情况,决定非线性函数的曲线.
log函数:x = lg(x)/lg(max)
Python实现
线性归一化
定义数组:x = numpy.array(x)
获取二维数组列方向的最大值:x.max(axis = 0)
获取二维数组列方向的最小值:x.min(axis = 0)
对二维数组进行线性归一化:
def max_min_normalization(data_value, data_col_max_values, data_col_min_values):
""" Data normalization using max value and min value
Args:
data_value: The data to be normalized
data_col_max_values: The maximum value of data's columns
data_col_min_values: The minimum value of data's columns
"""
data_shape = data_value.shape
data_rows = data_shape[0]
data_cols = data_shape[1]
for i in xrange(0, data_rows, 1):
for j in xrange(0, data_cols, 1):
data_value[i][j] = \
(data_value[i][j] - data_col_min_values[j]) / \
(data_col_max_values[j] - data_col_min_values[j])
标准差归一化
获取二维数组列方向的均值:x.mean(axis = 0)
获取二维数组列方向的标准差:x.std(axis = 0)
对二维数组进行标准差归一化:
def standard_deviation_normalization(data_value, data_col_means,
data_col_standard_deviation):
""" Data normalization using standard deviation
data_col_means: The means of data's columns
data_col_standard_deviation: The variance of data's columns
(data_value[i][j] - data_col_means[j]) / \
data_col_standard_deviation[j]
非线性归一化(以lg为例)
获取二维数组列方向的最大值:x.max(axis=0)
获取二维数组每个元素的lg值:numpy.log10(x)
获取二维数组列方向的最大值的lg值:numpy.log10(x.max(axis=0))
对二维数组使用lg进行非线性归一化:
def nonlinearity_normalization_lg(data_value_after_lg,
data_col_max_values_after_lg):
""" Data normalization using lg
data_value_after_lg: The data to be normalized
data_col_max_values_after_lg: The maximum value of data's columns
data_shape = data_value_after_lg.shape
data_value_after_lg[i][j] = \
data_value_after_lg[i][j] / data_col_max_values_after_lg[j]
以上就是土嘎嘎小编为大家整理的python归一化函数相关主题介绍,如果您觉得小编更新的文章只要能对粉丝们有用,就是我们最大的鼓励和动力,不要忘记讲本站分享给您身边的朋友哦!!