

排序的方法有:插入排序(直接插入排序、希尔排序),交换排序(冒泡排序、快速排序),选择排序(直接选择排序、堆排序),归并排序,分配排序(箱排序、基数排序)
快速排序的伪代码.
/
/使用快速排序方法对a[
:n-
]排序
从a[
]中选择一个元素作为m
i
d
l
e,该元素为支点
把余下的元素分割为两段left
和r
g
h
t,使得l
e
f
t中的元素都小于等于支点,而right
中的元素都大于等于支点
递归地使用快速排序方法对left
进行排序
递归地使用快速排序方法对right
所得结果为l
t
+
m
r
太久没看代码了,最近打算复习一下java,又突然想到了排序算法,就把几种常见的排序算法用java敲了一遍,这里统一将无序的序列从小到大排列.
选择排序是一种简单直观的排序算法.它的工作原理是:第一次从待排序的数据元素中选出最小的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小元素,继续放在下一个位置,直到待排序元素个数为0.
选择排序代码如下:
public void Select_sort(int[] arr) {
int temp,index;
for( int i=0;i10;i++) {
index = i;
for(int j = i + 1 ; j 10 ; j++) {
if(arr[j] arr[index])
index = j;
}
/*
temp = arr[i];
arr[i] = arr[index];
arr[index] = temp;
*/
swap(arr,i,index);
System.out.print("经过选择排序后:");
for(int i = 0 ; i 10 ; i++)
System.out.print( arr[i] +" ");
System.out.println("");
冒泡排序是一种比较基础的排序算法,其思想是相邻的元素两两比较,较大的元素放后面,较小的元素放前面,这样一次循环下来,最大元素就会归位,若数组中元素个数为n,则经过(n-1)次后,所有元素就依次从小到大排好序了.整个过程如同气泡冒起,所以呢被称作冒泡排序.
public void Bubble_sort(int[] arr) {
int temp;
for(int j = 0 ; j 10 - i - 1 ;j++) {
if(arr[j] arr[j+1]) {
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
swap(arr,j,j+1);
System.out.print("经过冒泡排序后:");
插入排序也是一种常见的排序算法,插入排序的思想是:创建一个与待排序数组等大的数组,每次取出一个待排序数组中的元素,然后将其插入到新数组中合适的位置,使新数组中的元素保持从小到大的顺序.
插入排序代码如下:
public void Insert_sort(int[] arr) {
int length = arr.length;
int[] arr_sort = new int[length];
int count = 0;
for(int i = 0;i length; i++) {
if(count == 0) {
arr_sort[0] = arr[0];
}else if(arr[i] = arr_sort[count - 1]) {
arr_sort[count] = arr[i];
}else if(arr[i] arr_sort[0]) {
insert(arr,arr_sort,arr[i],0,count);
}else {
for(int j = 0;j count - 1; j++) {
if(arr[i] = arr_sort[j] arr[i] arr_sort[j+1]) {
insert(arr,arr_sort,arr[i],j+1,count);
break;
count++;
System.out.print("经过插入排序后:");
System.out.print( arr_sort[i] +" ");
public void insert(int[] arr,int[] arr_sort,int value,int index,int count) {
for(int i = count; i index; i--)
arr_sort[i] = arr_sort[i-1];
arr_sort[index] = value;
快速排序的效率比冒泡排序算法有大幅提升.因为使用冒泡排序时,一次外循环只能归位一个值,有n个元素最多就要执行(n-1)次外循环.而使用快速排序时,一次可以将所有元素按大小分成两堆,也就是平均情况下需要logn轮就可以完成排序.
快速排序的思想是:每趟排序时选出一个基准值(这里以首元素为基准值),然后将所有元素与该基准值比较,并按大小分成左右两堆,然后递归执行该过程,直到所有元素都完成排序.
public void Quick_sort(int[] arr, int left, int right) {
if(left = right)
return ;
int temp,t;
int j = right;
int i = left;
temp = arr[left];
while(i j) {
while(arr[j] = temp i j)
j--;
while(arr[i] = temp i j)
i++;
if(i j) {
t = arr[i];
arr[i] = arr[j];
arr[j] = t;
arr[left] = arr[i];
arr[i] = temp;
Quick_sort(arr,left, i - 1);
Quick_sort(arr, i + 1, right);
归并排序是建立在归并操作上的一种有效的排序算法,归并排序对序列的元素进行逐层折半分组,然后从最小分组开始比较排序,每两个小分组合并成一个大的分组,逐层进行,最终所有的元素都是有序的.
public void Mergesort(int[] arr,int left,int right) {
if(right - left 0) {
int j = 0;
int k = 0;
for(int i = left;i = right;i++) {
arr_1[j++] = arr[i];
int i = 0;
int L1 = arr_1.length;
arr[k] = arr_1[i];
j++;
k++;
if(i == L1) {
for(int t = i;i L1;i++)
arr[k++] = arr_1[i];
归并排序这里我使用了left,right等变量,使其可以通用,并没有直接用数字表示那么明确,所以给出相关伪代码,便于理解.
Mergesort(arr[0...n-1])
//输入:一个可排序数组arr[0...n-1]
//输出:非降序排列的数组arr[0...n-1]
if n1
int i-0;j-0;k-0
while i
p span="" do="" j
arr[k] - arr_1[i]
i-i+1
k-k+1
if i=p
else copy arr_1[i...p-1] to arr[k...p+q-1]
package test_1;
import java.util.Scanner;
public class Test01 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int[] arr_1 = new int[10];
arr_1[i] = sc.nextInt();
Sort demo_1 = new Sort();
demo_1.Select_sort(arr_1);//-----------------------1
demo_1.Quick_sort(arr_1, 0 , arr_1.length - 1);
System.out.print("经过快速排序后:");
System.out.print( arr_1[i] +" ");
demo_1.Mergesort(arr_1,0,arr_1.length - 1);
System.out.print("经过归并排序后:");
class Sort {
public void swap(int arr[],int a, int b) {
int t;
t = arr[a];
arr[a] = arr[b];
arr[b] = t;
若有错误,麻烦指正,不胜感激.
冒泡排序:网页链接
所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作.排序算法,就是如何使得记录按照要求排列的方法.排序算法在很多领域得到相当地重视,尤其是在大量数据的处理方面.一个优秀的算法可以节省大量的资源.在各个领域中考虑到数据的各种限制和规范,要得到一个符合实际的优秀算法,得经过大量的推理和分析.
C++自带的algorithm库函数中提供了排序算法.
稳定的
桶排序(bucket sort)— O(n); 需要 O(k) 额外空间
计数排序(counting sort) — O(n+k); 需要 O(n+k) 额外空间
合并排序(merge sort)— O(nlog?n); 需要 O(n) 额外空间
鸽巢排序(Pigeonhole sort) — O(n+k); 需要 O(k) 额外空间
基数排序(radix sort)— O(n-k); 需要 O(n) 额外空间
图书馆排序— O(nlog?n) with high probability,需要 (1+★)n额外空间
不稳定的
希尔排序(shell sort)— O(nlog?n) 如果使用最佳的现在版本
组合排序— O(nlog?n)
堆排序(heapsort)— O(nlog?n)
平滑排序— O(nlog?n)
Introsort— O(nlog?n)
耐心排序— O(nlog?n+?k) 最坏情况时间,需要 额外的 O(n+?k) 空间,也需要找到最长的递增子串行(longest increasing subsequence)
不实用的
Bogo排序— O(nX?n!) 期望时间,无穷的最坏情况.
珠排序(Bead sort) — O(n) or O(√n),但需要特别的硬件
Pancake sorting— O(n),但需要特别的硬件
从数组第二个元素开始循环,比较其之前的元素有无比它大的,若有则往后移,最后将这个值放到正确位置
合并排序:
合并操作:
时间复杂度O(nlgn)
采用分治策略
排序一个数组A的全部元素,初始调用为QUICKSORT(A,1,A.length)
x为主元,并围绕x来分割A为两个数组
函数中,p为比x小的子数组的初始索引,i为比x小的子数组的最后索引,j为遍历除了x的数组元素的主索引
示例:
发生在分割中心选择了最大或最小的元素
分割中心每次都选到中值元素
此时为O(nlgn)
时间复杂度和最好情况相同
n为A中元素数目,k为A中 种类 数目
将A数组中出现的元素的次数记录在C数组中,
C数组中元素为 小于等于此索引 的A中元素出现的次数
最后将其表现为B数组,就排好序了
时间复杂度为O(n+k)
小范围整数排序O(n)
排序结果具有稳定性:对于相同值的元素,在原来数组中的先后顺序排序后得以保留
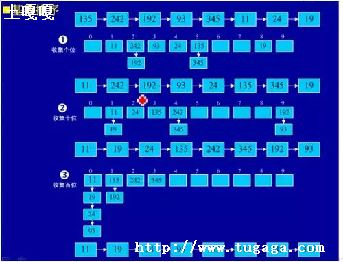
按照数字的基底一位位地排序
基底表示如下:
基数排序从低位开始进行稳定的增序排序,一直到最大位为止
将A数组的元素插入到B中
对B中每一个链进行插入排序(都说到这里了大家应该明白排序就对了)
平均情况下,时间复杂度为O(n)
因为数据是均匀、独立地分布在[0,1)之间,所以一般不会出现很多数落在同一个桶的情况.
以上就是土嘎嘎小编为大家整理的java插入排序伪代码相关主题介绍,如果您觉得小编更新的文章只要能对粉丝们有用,就是我们最大的鼓励和动力,不要忘记讲本站分享给您身边的朋友哦!!