

import?re
def?checklen(pwd):
def?checkContainUpper(pwd):
pattern?=?re.compile('[A-Z]+')
match?=?pattern.findall(pwd)
if?match:
return?True
else:
return?False
def?checkContainNum(pwd):
def?checkContainLower(pwd):
pattern?=?re.compile('[a-z]+')
def?checkSymbol(pwd):
def?checkPassword(pwd):
#判断密码长度是否合法
lenOK=checklen(pwd)
#判断是否包含大写字母
upperOK=checkContainUpper(pwd)
#判断是否包含小写字母
lowerOK=checkContainLower(pwd)
#判断是否包含数字
numOK=checkContainNum(pwd)
#判断是否包含符号
symbolOK=checkSymbol(pwd)
print(lenOK)
print(upperOK)
print(lowerOK)
print(numOK)
print(symbolOK)
return?(lenOK?and?upperOK?and?lowerOK?and?numOK?and?symbolOK)
def?main():
print('检测通过')
print('检测未通过')
if?__name__?==?'__main__':
main()
纯代码写就这样,还需要修改一下,业务中一般用正则表示:
import?re?
while?True:
line?=?raw_input("input:")
if?len(line)?==?0:
print?"NO"
print?'YES'
x=eval(input("请输入小于1000的整数:"))
print(x,"=",end="")
while x1:
if x%k==0:
? ? print(k,end="")
? ? x=x/k
? ? if x1:
? ? ? ? print("*",end="")
? ? k=k+1
对n进行分解质因数,应先找到一个最小的质数k,然后按下述步骤完成:
(1)如果这个质数恰等于n,则说明分解质因数的过程已经结束,打印出即可.
程序源代码:
#!/usr/bin/python
def reduceNum(n):
print '{} = '.format(n),
if not isinstance(n, int) or n = 0 :
print '请输入一个正确的数字 !'
exit(0)
elif n in [1] :
print '{}'.format(n)
while n not in [1] : # 循环保证递归
if n % index == 0:
n /= index # n 等于 n/index
if n == 1:
print index
else : # index 一定是素数
print '{} *'.format(index),
break
reduceNum(100)
以上实例输出结果为:
def?m(n):
ret?=?[]
while?n?1:
for?i?in?range(n-1):
if?n?%?k?==?0:
ret.append(k)
n?=?int(n?/?k)
print(ret)
至于如何处理成^就比较简单了,可以用 Counter 自己处理下.
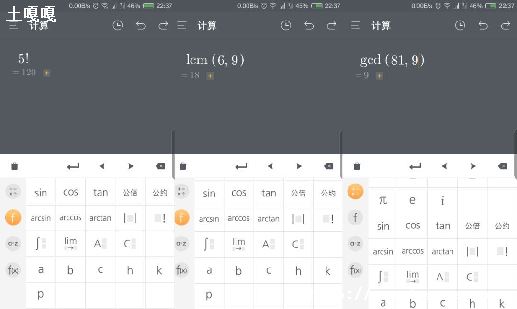
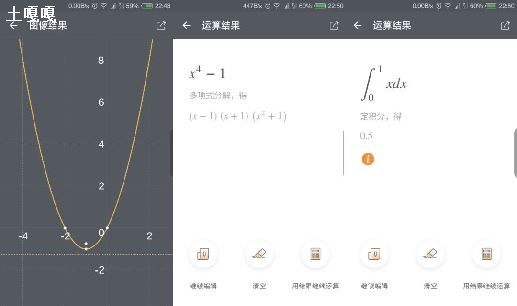
%号为取模运算.
from sympy import*导入库
x,y,z=symbols('x y z'),定义变量
init_printing(use_unicode=True)设置打印方式.
python的内部常量有pi,
x,y,z,t=symbols('x y z t')定义变量,
k, m, n = symbols('k m n', integer=True)定义三个整数变量.
f, g, h = symbols('f g h', cls=Function)定义的类型为函数.
cancel()is more efficient thanfactor().
asin(1)
trigsimp(sin(x)*tan(x)/sec(x))
x, y = symbols('x y', positive=True)正数,a, b = symbols('a b', real=True)实数,z, t, c = symbols('z t c')定义变量的方法.
powsimp(x**a*x**b)幂函数的乘法,不同幂的乘法,必须先定义a和b.powsimp(x**a*y**a)相同幂的乘法.
powsimp(t**c*z**c),注意,powsimp()refuses to do the simplification if it is not valid.
powsimp(t**c*z**c, force=True)这样的话就可以得到化简过的式子.声明强制进行化简.
powdenest((x**a)**b),powdenest((z**a)**b),powdenest((z**a)**b, force=True)
ln(x),x, y ,z= symbols('x y z', positive=True),n = symbols('n', real=True),
As withpowsimp()andpowdenest(),expand_log()has aforceoption that can be used to ignore assumptions.
logcombine(log(x) + log(y)),logcombine(n*log(x)),logcombine(n*log(z), force=True).
factorial(n)阶乘,binomial(n, k)等于c(n,k),gamma(z)伽马函数.
tan(x).rewrite(sin)得到用正弦表示的正切.factorial(x).rewrite(gamma)用伽马函数重写阶乘.
自定义函数
def list_to_frac(l):
expr = Integer(0)
for i in reversed(l[1:]):
expr += i
expr = 1/expr
return l[0] + expr
list_to_frac([x, y, z])结果为x + 1/z,这个结果是错误的.
使用cancel可以将生成的分式化简,frac = cancel(frac)化简为一个分数线的分式.
help("modules"),模块的含义,help("modules yourstr")模块中包含的字符串的意思.,
help("topics"),import os.path + help("os.path"),help("list"),help("open")
定义
fromsympyimport*
x,y,z=symbols('x y z')
init_printing(use_unicode=True)
limit(sin(x)/x,x,0),not-a-number表示nan算不出来,limit(expr, x, oo),,expr = Limit((cos(x) - 1)/x, x, 0),expr.doit()连用.左右极限limit(1/x, x, 0, '+'),limit(1/x, x, 0, '-')..
N=Matrix([0,1,1])
M*N符合矩阵的乘法.M.shape显示矩阵的行列数.
M.row(0)获取M的第0行.M.col(-1)获取倒数第一列.
[-1, 0, 0, 0],
[ 0, 1, 1, 0],
一行一行显示,,M.det()求行列式.M.rref()矩阵化简.得到结果为Matrix([
[0, 0,? 0,? 0]]), [0, 1]).
Columnspace
P, D = M.diagonalize(),P得Matrix([
[0, 1, 1,? 0],
[1, 1, 1, -1],
[1, 1, 1,? 0],
[1, 1, 0,? 1]]),,D为Matrix([
P*D*P**-1 == M返回为True.lamda = symbols('lamda').
lamda = symbols('lamda')定义变量,p = M.charpoly(lamda)和factor(p)
from sympy import *
E**(I*pi)+1,可以看出,I和E,pi已将在sympy内已定义.
tmp = series(exp(I*x), x, 0, 10)和pprint(tmp)打印出来可读性好,print(tmp)可读性不好..pprint将公式用更好看的格式打印出来,,pprint( series( cos(x), x, 0, 10) )
用双重积分求解球的体积.
integrate(circle_area,(x,-r,r))再积分即可.
expression.sub([(x,y),(y,x)])又换到原来的状况了.
expression.subs(x, y),,将算式中的x替换成y..
expression.subs({x:y,u:v}) : 使用字典进行多次替换..
expression.subs([(x,y),(u,v)]) : 使用列表进行多次替换..
n?=?int(input('please?enter?a?number:'))
if?n?%?i?==?0:
n?=?n?//?i
if?n?==?1:
print(i)
print(i,?'*',?end='?')