

不一样,插入的值是两个数的和
def?triangles(max):
L?=?[1]
n?=?0
while(nmax):
n?=?n+1
L=[1,1]
yield?L
else:
i?=?1
L1?=?[1,1]
L1.insert(i,L[i-1]+L[i])
i=i+1
L?=?L1
print?n
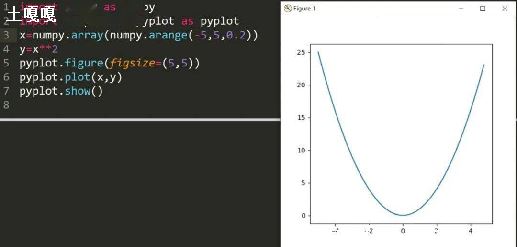
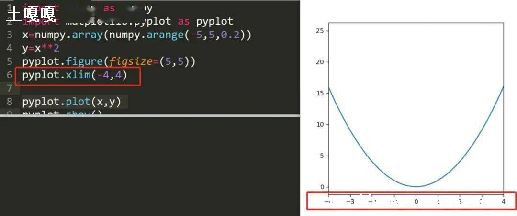
用Python输出一个杨辉三角的例子
这篇文章主要介绍了用Python和erlang输出一个杨辉三角的例子,同时还提供了一个erlang版杨辉三角,需要的朋友可以参考下
关于杨辉三角是什么东西,右转维基百科:杨辉三角
稍微看一下直观一点的图:
代码如下:
杨辉三角有以下几个特点:
每一项的值等于他左上角的数和右上角的数的和,如果左上角或者右上角没有数字,就按0计算.
第N层项数总比N-1层多1个
def _yanghui_trangle(n, result):
if n == 1:
return [1]
return [sum(i) for i in zip([0] + result, result + [0])]
稍微完善一下代码:
def yanghui_trangle(n):
pre_result = []
for i in xrange(n):
pre_result = _yanghui_trangle(i + 1, pre_result)
yield pre_result
if __name__ == "__main__":
print line
_yanghui_trangle可以用lambda的方式简写,但是可读性感觉会变差,所以还是保持现状好了.
tips: 上面的程序并没有考虑数据格式化的问题,也就是说输出不是完美的三角形.
鉴于最近在学习erlang,补上一个erlang版本的,性能上没有测试过,不过还是要惊叹于函数式语言的表达能力:
-module(yanghui).
-author(lfyzjck).
-export([triangle/1]).
triangle_next(P) -
lists:zipwith(fun(X, Y) - X+Y end, [0|P], P ++ [0]).
triangle(1) -
[[1]];
triangle(N) -
L = triangle(N - 1),
[H|_] = L,
[triangle_next(H)|L].
程序输出需要实现如下效果:
[1]
[1,1]
......
方法:迭代,生成器
def triangles() L = [1] while True: yiled L L =[1] + [L[i] + L[I+1] for i in range(len(L)-1)] + [1] n = 0 for t in triangles(): print(t) n += 1 if n == 10: break
实现逻辑:
①由于yield为生成器中断输出,所以有了第一个次输出为[1]
以此类推即可
[1, 1]
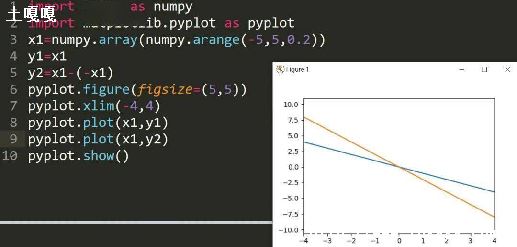
经过观察你就会发现这个列表推导式[L[i-1] + L[i] for i in range(len(L))]是产生每一行的杨辉三角数据的.
L[i-1]+L[i]是根据前一行指定索引位置的杨辉三角数据,产生新的一行的数据
杨辉三角,是二项式系数在三角形中的一种几何排列.
前提:每行端点与结尾的数为1.
每个数等于它上方两数之和.
每行数字左右对称,由1开始逐渐变大.
第n行的数字有n项.
第n行的m个数可表示为
C(n-1,m-1),即为从n-1个不同元素中取m-1个元素的组合数.
第n行的第m个数和第n-m+1个数相等
,为组合数性质之一.
每个数字等于上一行的左右两个数字之和.可用此性质写出整个杨辉三角.即第n+1行的第i个数等于第n行的第i-1个数和第i个数之和,这也是组合数的性质之一.即
C(n+1,i)=C(n,i)+C(n,i-1).
将各行数字相排列,可得11的n-1(n为行数)次方:1=11^0;
①.1=11^1;
完整代码:
#!/usr/bin/python
#
__author__
=
'cy'
#输出杨辉三角数值表
def
triangle(num):
#初始表值为[1]
triangle=[[1]]
[1],
[1]]
for
i
in
num+1):
triangle.append([1]*i)
#改变triangle表的值,eg:
j
range(1,
i-1):
triangle[i-1][j]
return
triangle
#格式化输出(输出的是一个表)
printtriangle(triangle,
width):
#列宽
column
len(triangle[-1])*width
sublist
triangle:
result
[]
contents
sublist:
#控制间距
result.append('{0:^{1}}'.format(str(contents),
width))
#控制缩进,{0:^{1}}:空格在两边补齐空位'^'居中对齐,':'号后面带填充的字符
print('{0:^{1}}'.format(''.join(result),
column))
#启动函数
if
__name__
==
'__main__':
#输入整数
num
int(input('How
many
rows
do
you
want:'))
#打印信息
"The
as
follows:"
triangle(num)
width
width)
使用python实现杨辉三角
python教程-生成器
杨辉三角的特点:
①每行端点与结尾的数为1
知道这三个特点即可
使用python列表生成式:
当 n=0 时, n-1=-1 ,这时候取倒数第一个元素 0 ,所以 1+0 = 1
剩下的元素就是 n + (n-1) = 新的元素
最后输出:
以上就是土嘎嘎小编为大家整理的杨辉三角函数Python相关主题介绍,如果您觉得小编更新的文章只要能对粉丝们有用,就是我们最大的鼓励和动力,不要忘记讲本站分享给您身边的朋友哦!!