

处理过与时间有关的数据的人都知道,差分变化经常用来使得结果更加直观.在这篇文章里将会教你如何用Python来实现这一目的,读完这篇文章,你将会掌握以下技能:
①.、知道什么是差分变换以及滞后差分和差分阶数的设置
所以,让我们赶紧开始吧!
为什么要对时间序列数据进行差分?
首先来看下为什么要对数据进行差分变化,差分变化可以消除数据对时间的依赖性,也就是降低时间对数据的影响,这些影响通常包括数据的变化趋势以及数据周期性变化的规律.进行差分操作时,一般用现在的观测值减去上个时刻的值就得到差分结果,就是这么简单,按照这种定义可以计算一系列的差分变换.
滞后差分
连续观测值之间的差分变换叫做一阶滞后差分.滞后差分的步长需要根据数据的时间结构做调整,例如对于周期性变化的数据,这个时间步长就是数据变化的周期.
差分阶数
在进行一次差分之后,时间项的作用并没有完全去掉,将会继续对差分结果进行差分变化,直到完全消除时间项的影响因素为止,这个过程中进行的差分操作次数就称为差分阶数.
洗发水销售数据
下面的代码将会导入数据并将结果画成折线图,如下所示:
手动差分
在这一部分中,我们将会自定义一个函数来实现差分变换,这个函数将会对提供的数据进行遍历并根据指定的时间间隔进行差分变换.具体代码如下:
从上面的代码中可以看到该函数将会根据指定的时间间隔来对数据进行变换,一般来说,通常会计算间隔一个数据的差分,这样的结果比较可靠.当然,我们也可以将上面的函数进行一定的改进,加入差分阶数的指定.
下面将这函数应用到上面洗发水销售的数据中去,运行之后绘出下面的图,具体如下:
自动差分
Pandas库里提供了一个函数可以自动计算数据的差分,这个函数是diff(),输入的数据是"series'或"DataFrame'类型的,像前面自定义函数那样,我们也可以指定差分的时间间隔,不过今天这一节这个参数叫做周期.
下面的例子是用Pandas内置函数来计算差分的,数据类型是series的,使用Pandas内置函数的好处是代码工作量减少了不少,而且绘出的图中包含更详细的信息,具体效果如下:
总结
读完本文想必你已经学会用python来实现对数据的差分了,尤其是对差分的概念,手动差分,以及使用Pandas内置函数进行差分都有所了解了.如果有什么好的想法欢迎在评论栏里留下.
python的求
标准差
的函数是std,是numpy库的成员,
如果非要
用sd函数求标准差,也不是不行(from
numpy
import
std
as
sd).其参数是所需求标准差的矩阵或列表,
返回值
即标准差.示范如下:
np;
from
sd;
print([1,
① 常用函数库
scipy包中的stats模块和statsmodels包是python常用的数据分析工具,scipy.stats以前有一个models子模块,后来被移除了.这个模块被重写并成为了现在独立的statsmodels包.
scipy的stats包含一些比较基本的工具,比如:t检验,正态性检验,卡方检验之类,statsmodels提供了更为系统的统计模型,包括线性模型,时序分析,还包含数据集,做图工具等等.
(1) 用途
夏皮罗维尔克检验法 (Shapiro-Wilk) 用于检验参数提供的一组小样本数据线是否符合正态分布,统计量越大则表示数据越符合正态分布,但是在非正态分布的小样本数据中也经常会出现较大的W值.需要查表来估计其概率.由于原假设是其符合正态分布,所以当P值小于指定显著水平时表示其不符合正态分布.
正态性检验是数据分析的第一步,数据是否符合正态性决定了后续使用不同的分析和预测方法,当数据不符合正态性分布时,我们可以通过不同的转换方法把非正太态数据转换成正态分布后再使用相应的统计方法进行下一步操作.
科尔莫戈罗夫检验(Kolmogorov-Smirnov test),检验样本数据是否服从某一分布,仅适用于连续分布的检验.下例中用它检验正态分布.
方差反映了一组数据与其平均值的偏离程度,方差齐性检验用以检验两组或多组数据与其平均值偏离程度是否存在差异,也是很多检验和算法的先决条件.
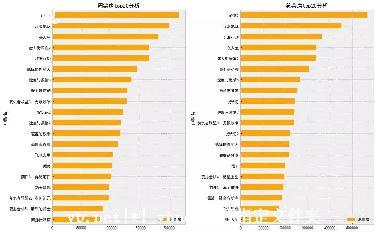
最常用的两变量相关性分析,是用作图描述相关性,图的横轴是一个变量,纵轴是另一变量,画散点图,从图中可以直观地看到相关性的方向和强弱,线性正相关一般形成由左下到右上的图形;负面相关则是从左上到右下的图形,还有一些非线性相关也能从图中观察到.
从图中可以看到明显的正相关趋势.
皮尔森相关系数(Pearson correlation coefficient)是反应两变量之间线性相关程度的统计量,用它来分析正态分布的两个连续型变量之间的相关性.常用于分析自变量之间,以及自变量和因变量之间的相关性.
斯皮尔曼等级相关系数(Spearman's correlation coefficient for ranked data ),它主要用于评价顺序变量间的线性相关关系,在计算过程中,只考虑变量值的顺序(rank, 值或称等级),而不考虑变量值的大小.常用于计算类型变量的相关性.
返回结果的第一个值为相关系数表示线性相关程度,本例中correlation趋近于1表示正相关.第二个值为p-value,p-value越小,表示相关程度越显著.
单样本T检验,用于检验数据是否来自一致均值的总体,T检验主要是以均值为核心的检验.注意以下几种T检验都是双侧T检验.
由于比较两组数据是否来自于同一正态分布的总体.注意:如果要比较的两组数据不满足方差齐性, 需要在ttest_ind()函数中添加参数equal_var = False.
①.0. 配对样本T检验
配对样本T检验可视为单样本T检验的扩展,检验的对象由一群来自正态分布独立样本更改为二群配对样本观测值之差.它常用于比较同一受试对象处理的前后差异,或者按照某一条件进行两两配对分别给与不同处理的受试对象之间是否存在差异.
①.1. 单因素方差分析
方差分析(Analysis of Variance,简称ANOVA),又称F检验,用于两个及两个以上样本均数差别的显著性检验.方差分析主要是考虑各组之间的平均数差别.
单因素方差分析(One-wayAnova),是检验由单一因素影响的多组样本某因变量的均值是否有显著差异.
当因变量Y是数值型,自变量X是分类值,通常的做法是按X的类别把实例成分几组,分析Y值在X的不同分组中是否存在差异.
当有两个或者两个以上自变量对因变量产生影响时,可以用多因素方差分析的方法来进行分析.它不仅要考虑每个因素的主效应,还要考虑因素之间的交互效应.
上面介绍的T检验是参数检验,卡方检验是一种非参数检验方法.相对来说,非参数检验对数据分布的要求比较宽松,并且也不要求太大数据量.卡方检验是一种对计数资料的假设检验方法,主要是比较理论频数和实际频数的吻合程度.常用于特征选择,比如,检验男人和女人在是否患有高血压上有无区别,如果有区别,则说明性别与是否患有高血压有关,在后续分析时就需要把性别这个分类变量放入模型训练.
基本数据有R行C列, 故通称RC列联表(contingency table), 简称RC表,它是观测数据按两个或更多属性(定性变量)分类时所列出的频数表.
单变量统计描述是数据分析中最简单的形式,其中被分析的数据只包含一个变量,不处理原因或关系.单变量分析的主要目的是通过对数据的统计描述了解当前数据的基本情况,并找出数据的分布模型.
单变量数据统计描述从集中趋势上看,指标有:均值,中位数,分位数,众数;从离散程度上看,指标有:极差、四分位数、方差、标准差、协方差、变异系数,从分布上看,有偏度,峰度等.需要考虑的还有极大值,极小值(数值型变量)和频数,构成比(分类或等级变量).
此外,还可以用统计图直观展示数据分布特征,如:柱状图、正方图、箱式图、频率多边形和饼状图.
多元线性回归模型(multivariable linear regression model ),因变量Y(计量资料)往往受到多个变量X的影响,多元线性回归模型用于计算各个自变量对因变量的影响程度,可以认为是对多维空间中的点做线性拟合.
极差是指一组数据内的最大值和最小值之间的差异.
平均差是说明集中趋势的,标准差是说明一组数据的离中趋势的.
一组数据中各数据与平均数的差的平方和的平均数叫做这组数据的方差;
极差越大,平均差的代表性越小,反之亦然;标准差越大,平均差的代表性越小,反之亦然.
方差的算术平方根=标准差
python作为数据分析的利器,求极差、平均数、中位数、众数与方差是很常用的,然而,在python进行统计往往要使用外部的python库numpy,这个库不难装,然而,如果单纯只是求极差、平均数、中位数、众数与方差,还是自己写比较好,因为,给一个.py程序别人的机器,别人的机器上没有python库numpy,又要别人折腾一番,这很不好.不过看情况咯,如果你要处理上亿级的数据,还是配置一下外部的python库numpy吧.
先给大家回归一下极差、平均数、中位数、众数与方差是什么鬼:
①.、极差:最大值与最小值之差.它是标志值变动的最大范围.英文:range
公式:R=Xmax-Xmin(其中,Xmax为最大值,Xmin为最小值)
公式:
公式:从小到大排序为?则N为奇数时,N为偶数时,?
但是,如果有两个或两个以上个数出现次数都是最多的,那么这几个数都是这组数据的众数.
还有,如果所有数据出现的次数都一样,那么这组数据没有众数.
公式:或者(就是在<<概率论与数理统计>>中那条,方差就是平方的期望-期望的平方)
所以呢,根据上述的理论,得到如下的代码:
[python]?view plain?copy
import?time;
import?random;
class?Math:
#求极差
@staticmethod
def?range(l):
return?max(l)-min(l);
#求平均数
def?avg(l):
return?float(sum(l))/len(l);
#求中位数
def?median(l):
l=sorted(l);#先排序
else:
#求众数
def?mode(l):
#统计list中各个数值出现的次数
count_dict={};
for?i?in?l:
if?count_dict.has_key(i):
count_dict[i]+=1;
count_dict[i]=1;
#求出现次数的最大值
max_appear=0
for?v?in?count_dict.values():
if?vmax_appear:
max_appear=v;
if?max_appear==1:
return;
mode_list=[];
for?k,v?in?count_dict.items():
if?v==max_appear:
mode_list.append(k);
return?mode_list;
#求方差
def?variance(l):#平方的期望-期望的平方
s1=0;
ex=float(sum(l))/len(l);
s=0;
return?float(s)/len(l);
#主函数,测试
print?"极差为:{0}".format(Math.range(arr));
print?"中位数为:{0}".format(Math.median(arr));
print?"众数为:{0}".format(Math.mode(arr));
print;
#性能测试
arraylist=[];
for?i?in?range(1,1000000):
arraylist.append(i);
random.shuffle(arraylist);
time_start=time.time();
time_end=time.time();
print?"{0}s".format(time_end-time_start);
运行结果如下:
关于这个程序有几点说明的:
(1)开头引入time与random主要是为了最后部分测试两种求方差的方式那种性能较优使用,一般情况下使用上述我自定义的Math类,无须引入任何python包.
阅读全文